Hi, Sobat Zenius, kali ini gue akan membahas materi transformasi geometri nih atau lebih tepatnya rumus dilatasi matematika dan contoh soal beserta pembahasannya.
Sebelumnya kita pernah bahas translasi, refleksi, dan rotasi, sekarang gue akan bahas materi terakhir dari transformasi geometri, yaitu dilatasi. Mungkin istilah dilatasi terdengar asing, ya? Istilah dilatasi dapat memiliki makna pengembangan, pemuaian, pembesaran, atau perkalian.

Dalam materi kali ini, makna pembesaran dan perkalian adalah yang mendekati pembahasan kita, nih. Selanjutnya, jika gue lagi gak pake istilah dilatasi, gue akan menggunakan kata pembesaran atau perkalian, ya, guys.Yuk!
Jangan banyak ba-bi-bu lagi, langsung saja kita bahas, guys.
Konsep dan Pengertian Dilatasi
Eits, sabar dong jangan langsung ke rumus dilatasi ya. Kalian perlu tahu dulu, apa itu transformasi geometri.
Begini singkatnya, Transformasi adalah perubahan dan geometri adalah ilmu ukur atau cabang ilmu matematika yang membahas tentang garis, sudut, bidang, dan ruang. Jadi, dapat disimpulkan transformasi geometri ini membahas proses penentuan titik-titik baru dari suatu bangun.
Untuk dilatasi sendiri, sedikitnya sudah kita bahas di awal artikel ini, guys. Dilatasi itu dapat berarti transformasi yang mengubah suatu ukuran (memperbesar/memperkecil) suatu bangun geometri tanpa merubah bentuk bangunnya.
Jadi tergantung dilatasinya ya, bisa membesar 2 kali lipat, atau 3 kali lipat dan seterusnya.
Sebelum lanjut, udah punya aplikasi Zenius belum? Belajar lewat aplikasinya juga nggak kalah asyik, lho. Download aplikasi Zenius untuk belajar yang lebih seru ya dengan klik gambar di bawah ini.
Rumus Dilatasi
Perlu elo ketahui dulu nih dalam rumus dilatasi matematika adalah elemen-elemen yang ada di dalamnya. Pada contoh soal dilatasi biasanya diketahui titik pusatnya, kemudian titik (x,y) dan dilatasinya yang dilambangkan dengan nilai K.
Rumus dilatasi cukup mudah karena hanya mengalikan angka pada x dan y dengan nilai K.
(x, y) → (xˡ, yˡ) = (Kx, Ky)
Misalnya begini, elo punya sebuah segitiga dengan titik A berada di (2, 4), titik B berada di (2, 2), dan titik C berada di (4, 2).
Segitiga tersebut akan mengalami pembesaran atau dilatasi sebesar dua kali lipatnya (K = 2). Di mana letak titik-titiknya jika segitiga itu mengalami dilatasi dua kali lipat?
Rumus dan cara menjawabnya adalah sebagai berikut, Sobat Zenius.
A (2, 4) → Aˡ (4, 8)
B (2, 2) → Bˡ (4, 4)
C (4, 2) → Cˡ (8, 4)
Semua angka baik x maupun y akan dikalikan dengan K = 2.
Berikut adalah visualisasi dari contoh tersebut.
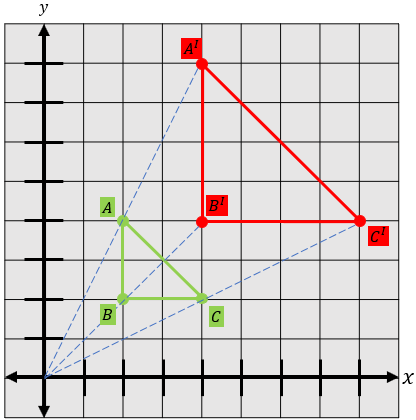
Cukup mudah kan? Dengan gambar di atas semoga elo dapat langsung mengerti dengan apa yang telah gue sampaikan.
Lalu, bagaimana jika titik pusatnya tidak berada pada titik 0 atau (0, 0)? Bagaimana jika titik pusatnya berada di (A, B)? Simak terus untuk menemukan jawabannya, ya. Untuk pembahasan yang lebih jelas, nanti gue juga akan sediakan contoh soal dilatasi.
Rumus Dilatasi dengan Faktor Skala K dan Pusat (A, B)
Nah, kita akan menjawab pertanyaan-pertanyaan sebelumnya. Jika jika titik pusatnya tidak berada pada titik (0, 0) atau titik pusatnya berada di (A, B), rumus dilatasi akan ditemukan dengan cara berikut, guys.
Perhatikan gambarnya dulu, ya!
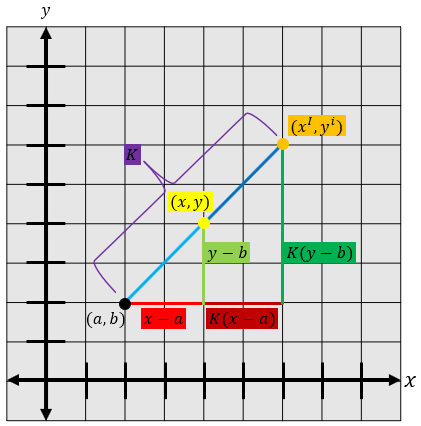
K(x – a) = xˡ – a
xˡ = K(x – a) + a
K(y – b) = yˡ – b
yˡ = K(y – b) + b
(x, y) → (xˡ, yˡ) = (K(x – a) + a, K(y – b) + b)
Jadi, rumus faktor skala dilatasi dengan skala K dan pusat (A, B) adalah seperti yang tercantum di atas. Sebuah transformasi dilatasi dengan faktor dilatasi kayak lebih susah dipahami ya? Bagaimana jika sekarang kita coba pakai pada contoh soal dilatasi?
Bagian ini kan yang paling elo tunggu-tunggu. Oke deh gak pake lama langsung saja kita sikat contoh soalnya








